DFS 알고리즘?
그래프 탐색 알고리즘 중 하나로, 특정 정점에서 시작하여 도달 가능한 정점까지 최대한 깊게 탐색한 후, 더 이상 뻗어 나아갈 수 없을 때 다시 가장 최근의 갈림길로 되돌아와 다른 경로를 탐색하는 방식이다.
이 알고리즘은 스택을 사용하여 구현할 수 있고, 재귀 호출을 통해서도 구현할 수 있다.
이 알고리즘을 통해 그래프의 모든 정점을 방문할 수 있다.

파이썬을 이용한 구현
# 그래프 클래스
class Graph:
def __init__(self, vertices):
self.V = vertices # 정점의 수
self.graph = {v: [] for v in range(vertices)} # 간선 딕셔너리
self.time = 0 # 탐색 시간(discovery/finish)을 체크하기 위한 필드
def add_edge(self, u, v):
self.graph[u].append(v) # (u, v) 간선을 등록
self.graph[v].append(u) # (v, u) 간선을 등록
# 탐색 전이면 WHITE, 탐색 중이면 GRAY, 탐색 완료면 BLACK
def dfs(self):
# 초기화
color = ['WHITE'] * self.V
d = [0] * self.V
f = [0] * self.V
pi = [None] * self.V
# 모든 정점에 대하여 방문
for u in range(self.V):
if color[u] == 'WHITE': # 방문하지 않은 정점에 대하여 탐색
self.dfsVisit(u, color, d, f, pi)
return d, f, pi
def dfsVisit(self, u, color, d, f, pi):
# u가 처음 발견 되었을 때 discovery time 설정
self.time += 1
d[u] = self.time
color[u] = 'GRAY'
# u에 인접한 정점 탐색
for v in self.graph[u]:
if color[v] == 'WHITE':
pi[v] = u # v의 이전 노드를 u로 설정
self.dfsVisit(v, color, d, f, pi)
# u에 대한 탐색이 끝났을 때
color[u] = 'BLACK'
self.time += 1
f[u] = self.time
# 예시
g = Graph(6)
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 3)
g.add_edge(2, 4)
g.add_edge(3, 5)
# DFS 수행
discovery_time, finish_time, predecessors = g.dfs()
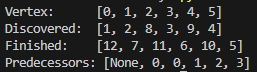
print("Vertex: ", list(range(6)))
print("Discovered: ", discovery_time)
print("Finished: ", finish_time)
print("Predecessors:", predecessors)결과는 아래와 같다.
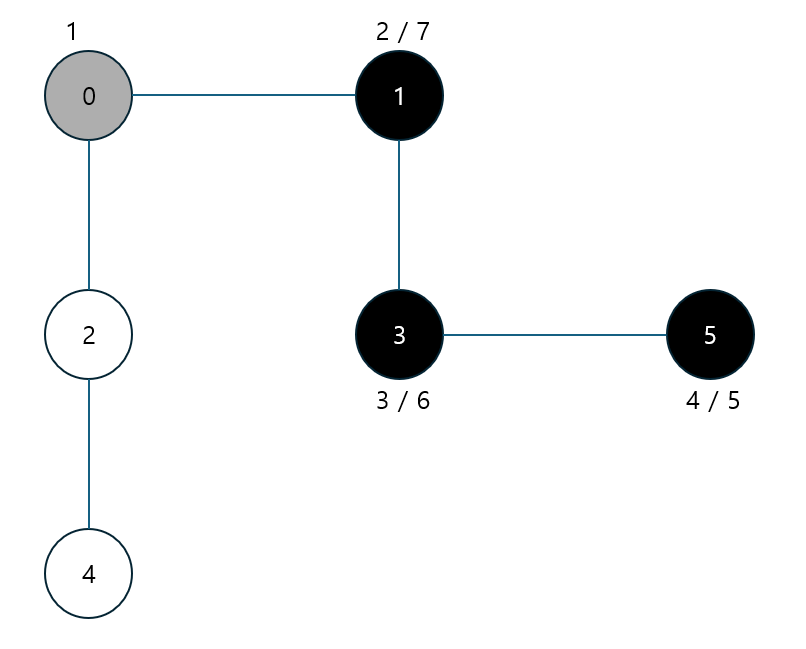
예시 세부 과정

초기화된 그래프의 상태이다.

0에서부터 탐색을 시작한다.

0에서 출발하여 갈 수 있는 곳까지 쭉 뻗어 나간다.

더 이상 갈 수 없으면 다시 가장 최근의 갈림길(0)으로 돌아간다.
0에서 다른 갈림길로 간다.
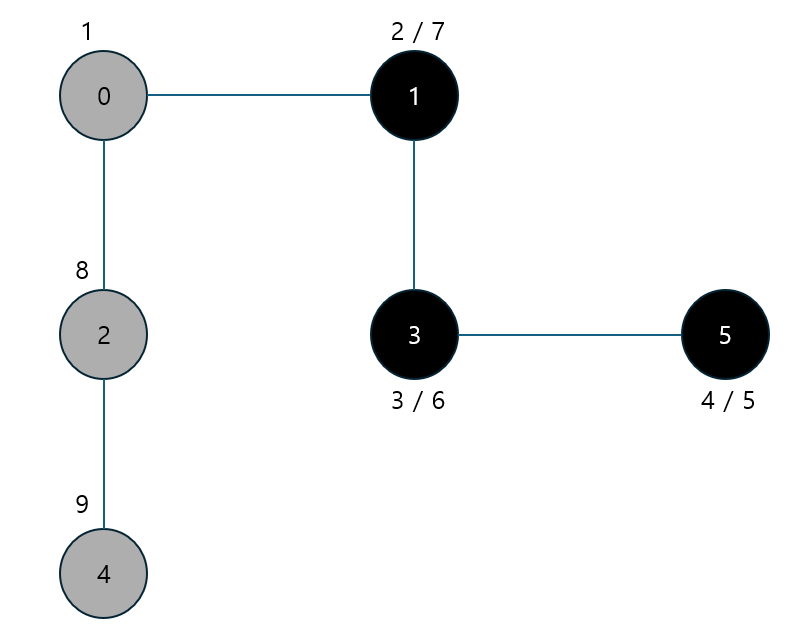
마찬가지로 갈 수 있을 때까지 뻗어간다.
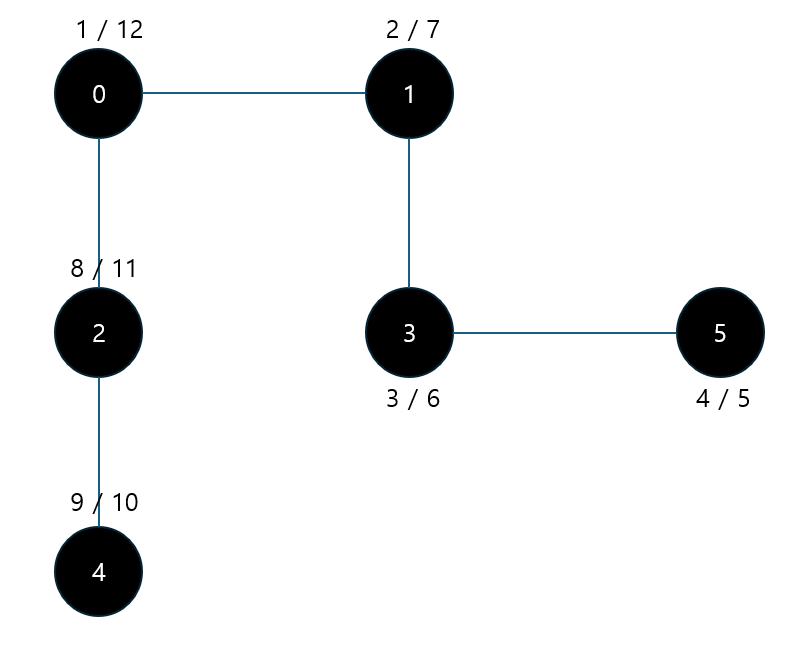
탐색 완료
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] 8퀸 문제 (0) | 2024.07.14 |
|---|---|
| [알고리즘] 하노이의 탑 (0) | 2024.07.14 |
| [알고리즘] 재귀 알고리즘(Recursion) - 1: 팩토리얼, 유클리드 호제법, 재귀 분석, 비재귀적 표현 (0) | 2024.07.06 |
| [알고리즘] 이진 검색 (Binary Search) (0) | 2024.06.28 |
| [알고리즘] 선형 검색 (linear search), 보초법(sentinel method)에 대하여 (0) | 2024.06.28 |
