하노이의 탑
작은 원반이 위에, 큰 원반이 아래에 위치하는 규칙을 지키면서 기둥 3개를 이용해서 원반을 옮기는 문제이다.
원반이 n개인 하노이탑 문제는 원반이 n-1개인 하노이탑 문제를 사용하여 재귀적으로 풀이할 수 있다.
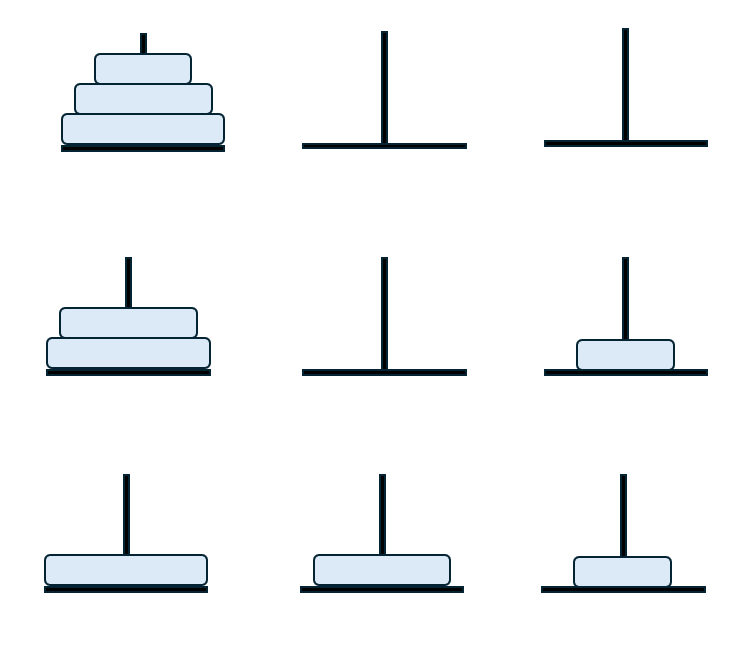

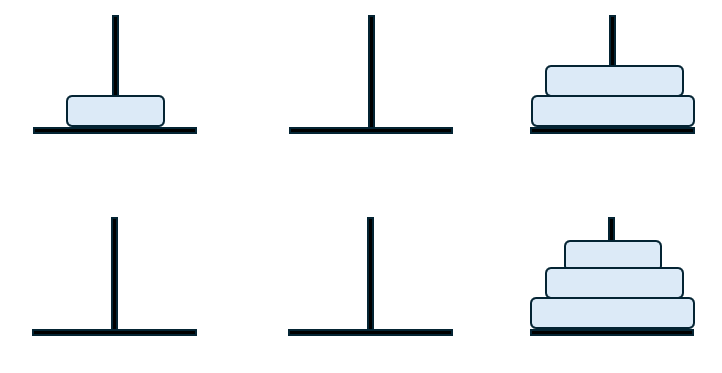
원반이 3개인 하노이 탑은 위와 같다.
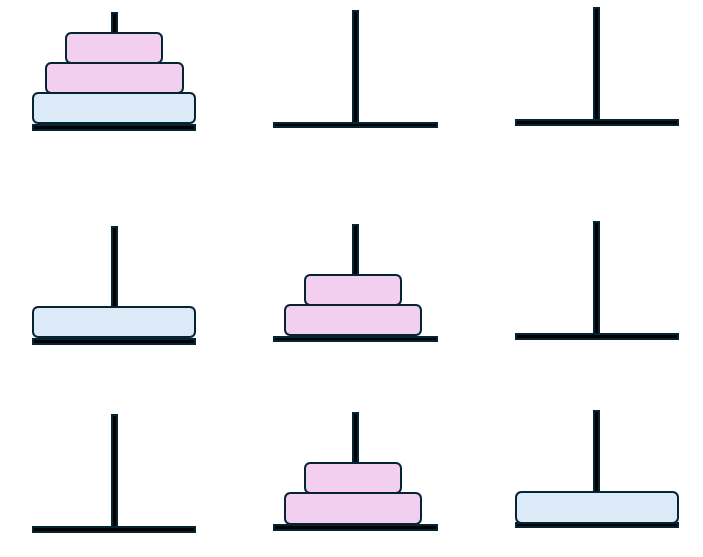

그리고, 이 과정에서 작은 원반 2개를 묶어서 생각할 수 있는데, 이 처럼 원반이 n개인 하노이탑 문제를 재귀적으로 풀이할 수 있다.
구현(기둥이 3개일 때)
# 하노이의 탑 구현하기
def move(no: int, x: int, y: int) -> None:
"""원반 no개를 x 기둥에서 y 기둥으로 옮김"""
if no > 1:
move(no - 1, x, 6 - x - y)
print(f'원반 [{no}]을(를) {x}기둥에서 {y}기둥으로 옮깁니다.')
if no > 1:
move(no - 1, 6 - x - y, y)
print('하노이 탑을 구현합니다.')
n = int(input('원반의 개수를 입력하세요.: '))
move(n, 1, 3) # 1기둥에 쌓인 원반 n개를 3기둥으로 옮김위 코드는 기둥이 3개일 때 성립한다.
이 코드에서 출발 기둥: x, 목표 기둥: y이다.
기둥이 3개이고 기둥 번호가 각각 1, 2, 3이라면 기둥 번호의 합이 6이므로, 나머지 기둥은 6-x-y로 표현할 수 있다.
참고 문헌
https://www.easyspub.co.kr/20_Menu/BookView/381/PUB
https://www.easyspub.co.kr/20_Menu/BookView/381/PUB
www.easyspub.co.kr
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] 8퀸 문제 (0) | 2024.07.14 |
|---|---|
| [알고리즘] 재귀 알고리즘(Recursion) - 1: 팩토리얼, 유클리드 호제법, 재귀 분석, 비재귀적 표현 (0) | 2024.07.06 |
| [알고리즘] 이진 검색 (Binary Search) (0) | 2024.06.28 |
| [알고리즘] 선형 검색 (linear search), 보초법(sentinel method)에 대하여 (0) | 2024.06.28 |
| [알고리즘] DFS(Depth First Search) 깊이 우선 탐색 (0) | 2024.06.28 |
