Binary Search Tree (BST)의 특징
- BST의 성능은 트리 높이에 의해서 결정된다.
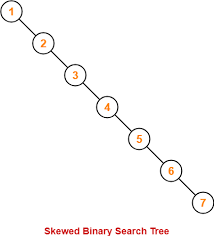
- 입력되는 값의 순서에 따라 트리가 균형을 이룰 수도 있지만, 균형이 깨질 수도 있다.
- 삽입/삭제 과정에서 최적의 경우에는 O(log n)의 시간 복잡도를 가지지만, 최악의 경우에는 O(n)의 시간 복잡도를 가진다.

AVL Tree (Adelson-Velsky and Landis Tree)
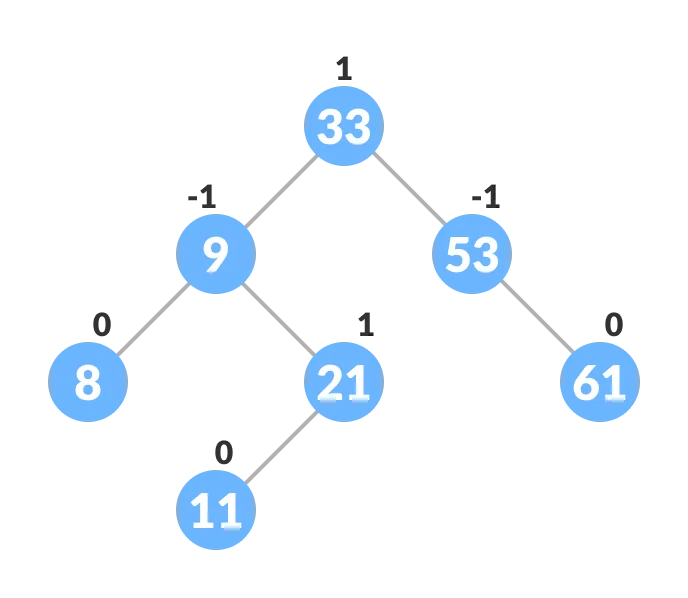
스스로 균형을 유지하는 트리를 AVL Tree라고 한다.
모든 노드에 대하여 각각의 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이가 1 이하이다.
C언어로 AVL Tree 구조체를 구현하면 다음과 같다.
typedef struct AVLNode {
int data;
struct AVLNode* left;
struct AVLNode* right;
int height; // BST와는 다르게 높이를 선언
} AVLNode;
Traverse(순회), Search(검색)은 이전 게시물 BST에서의 함수와 똑같다.
아래를 참고하자
https://swlin23.tistory.com/12
[자료구조] Binary Search Tree (BST) C언어로 구현하기 (검색, 삽입, 삭제)
Love IT! [자료구조] Binary Search Tree (BST) C언어로 구현하기 (검색, 삽입, 삭제) 본문 CS/자료구조 [자료구조] Binary Search Tree (BST) C언어로 구현하기 (검색, 삽입, 삭제) 1in 2024. 4. 9. 03:30
swlin23.tistory.com
AVL Tree Insertion
Insertion 함수의 처음은 BST insertion 함수와 모양이 비슷하다.
그러나 데이터를 넣고 서브트리의 height 값을 비교하면서 balanced 여부를 판단한다.
새로운 데이터를 삽입함으로 인해 기존 트리의 균형이 깨질 수 있다.
총 네가지 경우로 나눌 수 있다. (LL, LR, RR, RL)
이때 균형이 깨진 기준 노드를 z이라고 하자.
그리고 균형이 깨진 경로를 z-y-x 라고 하자.
1. z의 왼쪽 서브트리가 길고, 왼쪽 서브트리의 왼쪽이 길어진 경우(LL case)

왼쪽 서브트리의 왼쪽이 길어졌으므로, z(100) 기준 오른쪽으로 rotation을 해주면 된다.
z(100)를 오른쪽 아래로 보내고, y(50)를 오른쪽 위로 보내면 된다.
이 때, y(50)의 오른쪽 서브트리(75)를 z의 왼쪽 서브트리로 옮겨준다.
이를 코드로 구현하면 다음과 같다.
AVLNode* rightRotate(AVLNode *z) {
AVLNode* y = z->left; // z의 왼쪽 서브트리를 y라고 하기
AVLNode* T3 = y->right; // y의 오른족 서브트리를 T3라고 하기
z->left = T3; // z의 왼쪽을 y의 오른쪽 서브트리로 한다
y->right = z; // y의 오른쪽을 z로 한다.
z->height = max(height(z->left), height(z->right)) + 1;
y->height = max(height(y->left), height(y->right)) + 1;
return y;
}
2. z의 오른쪽 서브트리가 길고, 오른쪽 서브트리의 오른쪽이 길어진 경우(RR case)

오른쪽 서브트리의 오른쪽이 길어졌으므로, z 기준 왼쪽으로 rotation을 해주면 된다.
z를 왼쪽 아래로 보내고, y를 왼쪽 위로 보내면 된다.
이 때, y의 왼쪽 서브트리를 z의 오른쪽 서브트리로 옮겨준다.
이를 코드로 구현하면 다음과 같다.
AVLNode* leftRotate(AVLNode *z) {
AVLNode* y = z->right; // z의 오른쪽 서브트리를 y라고 하기
AVLNode* T3 = y->left; // y의 왼족 서브트리를 T2라고 하기
z->right = T3; // z의 오른쪽을 y의 왼쪽 서브트리로 한다
y->left = z; // y의 왼쪽을 z로 한다.
z->height = max(height(z->left), height(z->right)) + 1;
y->height = max(height(y->left), height(y->right)) + 1;
return y;
}
3. z의 왼쪽 서브트리가 길고, 왼쪽 서브트리의 오른쪽이 길어진 경우(LR case)

z 기준 왼쪽 서브트리가 길어졌을 때, 그 왼쪽 서브트리의 오른쪽이 길어진 경우
이때는 위와 방식이 다르다.
먼저, LR case를 LL case로 만들어 준 후, 오른쪽으로 rotation 한다.
4. z의 오른쪽 서브트리가 길고, 오른쪽 서브트리의 왼쪽이 길어진 경우(RL case)

3번과 유사한 과정을 거치는데, 이때는 RL case를 RR case로 만들어 준 후, 오른쪽으로 rotation 한다.
case 1, 2, 3, 4를 모두 고려하여 insertion 함수를 만들면 아래와 같다.
AVLNode* insert(AVLNode* node, int key) {
// 트리가 비었거나 삽입할 곳을 찾았을 때
if (node == NULL)
return(newAVLNode(key));
// LL or LR case
if (key < node->data) {
node->left = insert(node->left, key);
// 균형이 깨진 경우
if (height(node->left) - height(node->right) > 1) {
// LL case
if (key < node->left->data) {
return rightRotate(node);
}
// LR case
else {
AVLNode* y = node->left;
node->left = leftRotate(y);
return rightRotate(node);
}
}
}
// RR or RL case
if (key > node->data) {
node->right = insert(node->right, key);
// 균형이 깨진 경우
if (height(node->right) - height(node->left) > 1) {
// RR case
if (key > node->right->data) {
return leftRotate(node);
}
// RL case
else {
AVLNode* y = node->right;
rightRotate(y);
return leftRotate(node);
}
}
}
// 높이 수정 후 노드를 리턴
node->height = 1 + max(height(node->left), height(node->right));
return node;
}
AVL Tree Deletion
반대로, 어떤 노드가 삭제됨으로 인해 균형이 깨질 수 있다.
오른쪽 서브트리의 어떤 노드를 삭제하면, LL/LR case가 발생할 수 있다.
왼쪽 서브트리의 어떤 노드를 삭제하면, RR/RL case가 발생할 수 있다.
함수 구현은 다음과 같다.
AVLNode* delete(AVLNode* root, int key) {
// 트리가 비어있거나 찾으려는 값이 없을 때
if (root == NULL)
return NULL;
if (key > root->data)
root->right = delete(root->right, key);
else if (key < root->data)
root->left = delete(root->left, key);
else {
if (root->left == NULL && root->right == NULL) {
free(root);
return NULL;
}
else if (root->left == NULL || root->right == NULL) {
AVLNode* temp;
if (root->left == NULL)
temp = root->right;
else
temp = root->left;
free(root);
return temp;
}
else {
AVLNode* temp = FindMin(root->right);
root->data = temp->data;
root->right = delete(root->right, temp->data);
}
}
root->height = 1 + max(height(root->left), height(root->right));
// 오른쪽 데이터가 삭제된 경우(LL, LR case)
if (height(root->left) - height(root->right) > 1) {
if (height(root->left->left) >= height(root->left->right)) {
return rightRotate(root);
}
else {
AVLNode* y = root->left;
leftRotate(y);
return rightRotate(root);
}
}
// 왼쪽 데이터가 삭제된 경우(RR, RL case)
else if (height(root->right) - height(root->left) > 1) {
if (height(root->right->right) >= height(root->right->left)) {
return leftRotate(root);
}
else {
AVLNode* y = root->right;
rightRotate(y);
return leftRotate(root);
}
}
return root;
}'CS > 자료구조' 카테고리의 다른 글
| [자료구조] 레드-블랙 트리 삽입 연산 (0) | 2024.05.24 |
|---|---|
| [자료구조] Red-Black Tree 레드-블랙 트리 (0) | 2024.05.24 |
| [자료구조] 배열과 동적 메모리 할당 in C언어 (0) | 2024.04.13 |
| [자료구조] Binary Search Tree (BST) C언어로 구현하기 (검색, 삽입, 삭제) (0) | 2024.04.09 |
| [자료구조] Binary-Tree 이진 트리 C언어로 구현하기 (0) | 2024.04.06 |
Binary Search Tree (BST)의 특징
- BST의 성능은 트리 높이에 의해서 결정된다.
- 입력되는 값의 순서에 따라 트리가 균형을 이룰 수도 있지만, 균형이 깨질 수도 있다.
- 삽입/삭제 과정에서 최적의 경우에는 O(log n)의 시간 복잡도를 가지지만, 최악의 경우에는 O(n)의 시간 복잡도를 가진다.


AVL Tree (Adelson-Velsky and Landis Tree)
스스로 균형을 유지하는 트리를 AVL Tree라고 한다.
모든 노드에 대하여 각각의 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이가 1 이하이다.

C언어로 AVL Tree 구조체를 구현하면 다음과 같다.
typedef struct AVLNode {
int data;
struct AVLNode* left;
struct AVLNode* right;
int height; // BST와는 다르게 높이를 선언
} AVLNode;
Traverse(순회), Search(검색)은 이전 게시물 BST에서의 함수와 똑같다.
아래를 참고하자
https://swlin23.tistory.com/12
[자료구조] Binary Search Tree (BST) C언어로 구현하기 (검색, 삽입, 삭제)
Love IT! [자료구조] Binary Search Tree (BST) C언어로 구현하기 (검색, 삽입, 삭제) 본문 CS/자료구조 [자료구조] Binary Search Tree (BST) C언어로 구현하기 (검색, 삽입, 삭제) 1in 2024. 4. 9. 03:30
swlin23.tistory.com
AVL Tree Insertion
Insertion 함수의 처음은 BST insertion 함수와 모양이 비슷하다.
그러나 데이터를 넣고 서브트리의 height 값을 비교하면서 balanced 여부를 판단한다.
새로운 데이터를 삽입함으로 인해 기존 트리의 균형이 깨질 수 있다.
총 네가지 경우로 나눌 수 있다. (LL, LR, RR, RL)
이때 균형이 깨진 기준 노드를 z이라고 하자.
그리고 균형이 깨진 경로를 z-y-x 라고 하자.
1. z의 왼쪽 서브트리가 길고, 왼쪽 서브트리의 왼쪽이 길어진 경우(LL case)

왼쪽 서브트리의 왼쪽이 길어졌으므로, z(100) 기준 오른쪽으로 rotation을 해주면 된다.
z(100)를 오른쪽 아래로 보내고, y(50)를 오른쪽 위로 보내면 된다.
이 때, y(50)의 오른쪽 서브트리(75)를 z의 왼쪽 서브트리로 옮겨준다.
이를 코드로 구현하면 다음과 같다.
AVLNode* rightRotate(AVLNode *z) {
AVLNode* y = z->left; // z의 왼쪽 서브트리를 y라고 하기
AVLNode* T3 = y->right; // y의 오른족 서브트리를 T3라고 하기
z->left = T3; // z의 왼쪽을 y의 오른쪽 서브트리로 한다
y->right = z; // y의 오른쪽을 z로 한다.
z->height = max(height(z->left), height(z->right)) + 1;
y->height = max(height(y->left), height(y->right)) + 1;
return y;
}
2. z의 오른쪽 서브트리가 길고, 오른쪽 서브트리의 오른쪽이 길어진 경우(RR case)

오른쪽 서브트리의 오른쪽이 길어졌으므로, z 기준 왼쪽으로 rotation을 해주면 된다.
z를 왼쪽 아래로 보내고, y를 왼쪽 위로 보내면 된다.
이 때, y의 왼쪽 서브트리를 z의 오른쪽 서브트리로 옮겨준다.
이를 코드로 구현하면 다음과 같다.
AVLNode* leftRotate(AVLNode *z) {
AVLNode* y = z->right; // z의 오른쪽 서브트리를 y라고 하기
AVLNode* T3 = y->left; // y의 왼족 서브트리를 T2라고 하기
z->right = T3; // z의 오른쪽을 y의 왼쪽 서브트리로 한다
y->left = z; // y의 왼쪽을 z로 한다.
z->height = max(height(z->left), height(z->right)) + 1;
y->height = max(height(y->left), height(y->right)) + 1;
return y;
}
3. z의 왼쪽 서브트리가 길고, 왼쪽 서브트리의 오른쪽이 길어진 경우(LR case)

z 기준 왼쪽 서브트리가 길어졌을 때, 그 왼쪽 서브트리의 오른쪽이 길어진 경우
이때는 위와 방식이 다르다.
먼저, LR case를 LL case로 만들어 준 후, 오른쪽으로 rotation 한다.
4. z의 오른쪽 서브트리가 길고, 오른쪽 서브트리의 왼쪽이 길어진 경우(RL case)

3번과 유사한 과정을 거치는데, 이때는 RL case를 RR case로 만들어 준 후, 오른쪽으로 rotation 한다.
case 1, 2, 3, 4를 모두 고려하여 insertion 함수를 만들면 아래와 같다.
AVLNode* insert(AVLNode* node, int key) {
// 트리가 비었거나 삽입할 곳을 찾았을 때
if (node == NULL)
return(newAVLNode(key));
// LL or LR case
if (key < node->data) {
node->left = insert(node->left, key);
// 균형이 깨진 경우
if (height(node->left) - height(node->right) > 1) {
// LL case
if (key < node->left->data) {
return rightRotate(node);
}
// LR case
else {
AVLNode* y = node->left;
node->left = leftRotate(y);
return rightRotate(node);
}
}
}
// RR or RL case
if (key > node->data) {
node->right = insert(node->right, key);
// 균형이 깨진 경우
if (height(node->right) - height(node->left) > 1) {
// RR case
if (key > node->right->data) {
return leftRotate(node);
}
// RL case
else {
AVLNode* y = node->right;
rightRotate(y);
return leftRotate(node);
}
}
}
// 높이 수정 후 노드를 리턴
node->height = 1 + max(height(node->left), height(node->right));
return node;
}
AVL Tree Deletion
반대로, 어떤 노드가 삭제됨으로 인해 균형이 깨질 수 있다.
오른쪽 서브트리의 어떤 노드를 삭제하면, LL/LR case가 발생할 수 있다.
왼쪽 서브트리의 어떤 노드를 삭제하면, RR/RL case가 발생할 수 있다.
함수 구현은 다음과 같다.
AVLNode* delete(AVLNode* root, int key) {
// 트리가 비어있거나 찾으려는 값이 없을 때
if (root == NULL)
return NULL;
if (key > root->data)
root->right = delete(root->right, key);
else if (key < root->data)
root->left = delete(root->left, key);
else {
if (root->left == NULL && root->right == NULL) {
free(root);
return NULL;
}
else if (root->left == NULL || root->right == NULL) {
AVLNode* temp;
if (root->left == NULL)
temp = root->right;
else
temp = root->left;
free(root);
return temp;
}
else {
AVLNode* temp = FindMin(root->right);
root->data = temp->data;
root->right = delete(root->right, temp->data);
}
}
root->height = 1 + max(height(root->left), height(root->right));
// 오른쪽 데이터가 삭제된 경우(LL, LR case)
if (height(root->left) - height(root->right) > 1) {
if (height(root->left->left) >= height(root->left->right)) {
return rightRotate(root);
}
else {
AVLNode* y = root->left;
leftRotate(y);
return rightRotate(root);
}
}
// 왼쪽 데이터가 삭제된 경우(RR, RL case)
else if (height(root->right) - height(root->left) > 1) {
if (height(root->right->right) >= height(root->right->left)) {
return leftRotate(root);
}
else {
AVLNode* y = root->right;
rightRotate(y);
return leftRotate(root);
}
}
return root;
}'CS > 자료구조' 카테고리의 다른 글
| [자료구조] 레드-블랙 트리 삽입 연산 (0) | 2024.05.24 |
|---|---|
| [자료구조] Red-Black Tree 레드-블랙 트리 (0) | 2024.05.24 |
| [자료구조] 배열과 동적 메모리 할당 in C언어 (0) | 2024.04.13 |
| [자료구조] Binary Search Tree (BST) C언어로 구현하기 (검색, 삽입, 삭제) (0) | 2024.04.09 |
| [자료구조] Binary-Tree 이진 트리 C언어로 구현하기 (0) | 2024.04.06 |
