Binary Search Tree?
왼쪽의 모든 노드보다는 크고, 오른쪽의 모든 노드보다는 작은 이진 트리
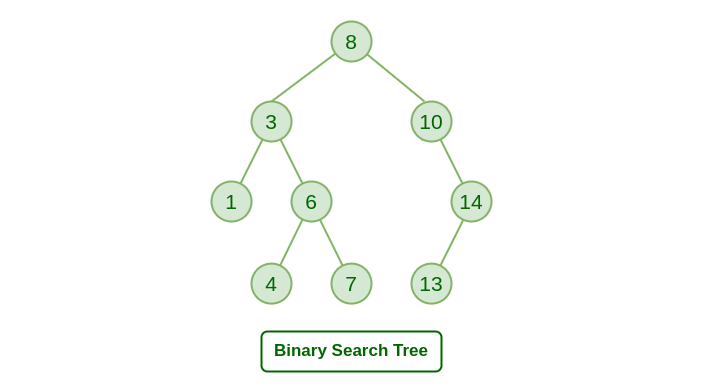
장점
- search 시에 key를 찾기가 쉬움
- 삽입/삭제가 쉬움
C언어로 구현하기(Search, Insert, Delete)
#include <stdio.h>
#include <stdlib.h>
// bst 구조체 선언
typedef struct BstNode {
int key;
struct BstNode *left, *right;
} BstNode;
1. Search
1. 최솟값 Search
// bst에서 최솟값 찾기
BstNode* findMin(BstNode* root) {
if (root == NULL)
return NULL;
else if (root->left != NULL)
return findMin(root->left);
return root;
}
2. 최댓값 Search
BstNode* findMax(BstNode* root) {
if (root == NULL)
return NULL;
else if (root->right != NULL)
return findMax(root->right);
return root;
}
3. 원하는 key값 Search
// bst에서 key 찾기
BstNode* searchNode(BstNode* root, int target) {
if (root == NULL)
return NULL;
if (root->key > target)
return searchNode(root->left, target);
else if (root->key < target)
return searchNode(root->right, target);
else
return root;
}
2. Insert
// key를 삽입
BstNode* insertNode(BstNode* node, int value) {
// 트리가 비어있으면 새로운 노드를 만듦
if (node == NULL) {
// 해당 위치까지 이동 했으니 그 곳에서 노드를 만듦
BstNode* tmp = (BstNode*)malloc(sizeof(BstNode));
tmp->key = value;
tmp->left = tmp->right = NULL;
return tmp;
}
// Search 과정과 비슷함
if (value < node->key)
node->left = insertNode(node->left, value);
else if (value > node->key)
node->right = insertNode(node->right, value);
else // 이미 key가 트리 안에 있으면
; // 아무 것도 하지 않음
return node;
}트리가 비어있는 경우는 처음부터 트리가 비어있었거나, 위치를 찾은 경우에 해당함
그 위치에서 tmp를 이용하여 노드를 만든다.
이후 재귀적 과정을 통해 노드가 연결 된다.
3. delete
// x값을 delete 과정
BstNode* deleteNode(BstNode* root, int x) {
if (root == NULL)
return NULL;
if (x > root->key)
root->right = delete(root->right);
else if (x < root->key)
root->left = delete(root->left);
else {
// x 노드에 자식이 0개일 경우
if (root->left == NULL && root->right == NULL) {
free(root);
return NULL;
}
// x 노드에 자식이 1개일 경우
else if (root->left == NULL && root->right == NULL) {
// tmp 선언하여 x 노드의 자식 노드를 저장함
BstNode* tmp;
// 오른쪽에 자식이 있는 경우
if (root->left == NULL)
tmp = root->right;
// 왼쪽에 자식이 있는 경우
else
tmp = root->left;
// x 노드 삭제
free(root);
return tmp;
}
// x 노드에 자식이 2개일 경우
else {
// x 노드의 오른쪽 서브트리의 최솟값을 찾아서 tmp에 저장함
BstNode* tmp = findMin(root->right);
// root의 값을 tmp 값으로 변경
root->key = tmp->key;
// 그 최솟값 노드를 삭제함
root->right = delete(root->right, tmp->key);
}
}
return root;
}삭제하고자 하는 노드의 자식 수에 따라 해결방법이 달라지므로 주의해야한다.
자식이 0개인 경우: 그냥 그 노드를 삭제하면 됨
자식이 1개인 경우: 그 노드의 자식 노드를 그 노드의 이전 노드와 이어야 함
자식이 2개인 경우: 그 노드의 오른쪽 서브트리의 최솟값을 그 노드의 값에 저장하고, 기존의 최솟값 노드는 제거하는 과정을 거쳐야 한다.
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] AVL Tree C언어로 구현하기 (Insertion, Delete) (0) | 2024.04.18 |
|---|---|
| [자료구조] 배열과 동적 메모리 할당 in C언어 (0) | 2024.04.13 |
| [자료구조] Binary-Tree 이진 트리 C언어로 구현하기 (0) | 2024.04.06 |
| [자료구조] Doubly Linked List (이중 연결 리스트) C언어로 구현하기 (0) | 2024.03.31 |
| [자료구조] Linked List (연결 리스트) C언어로 구현하기 (노드 순회, 검색, 삽입, 삭제) (0) | 2024.03.31 |
Binary Search Tree?
왼쪽의 모든 노드보다는 크고, 오른쪽의 모든 노드보다는 작은 이진 트리

장점
- search 시에 key를 찾기가 쉬움
- 삽입/삭제가 쉬움
C언어로 구현하기(Search, Insert, Delete)
#include <stdio.h>
#include <stdlib.h>
// bst 구조체 선언
typedef struct BstNode {
int key;
struct BstNode *left, *right;
} BstNode;
1. Search
1. 최솟값 Search
// bst에서 최솟값 찾기
BstNode* findMin(BstNode* root) {
if (root == NULL)
return NULL;
else if (root->left != NULL)
return findMin(root->left);
return root;
}
2. 최댓값 Search
BstNode* findMax(BstNode* root) {
if (root == NULL)
return NULL;
else if (root->right != NULL)
return findMax(root->right);
return root;
}
3. 원하는 key값 Search
// bst에서 key 찾기
BstNode* searchNode(BstNode* root, int target) {
if (root == NULL)
return NULL;
if (root->key > target)
return searchNode(root->left, target);
else if (root->key < target)
return searchNode(root->right, target);
else
return root;
}
2. Insert
// key를 삽입
BstNode* insertNode(BstNode* node, int value) {
// 트리가 비어있으면 새로운 노드를 만듦
if (node == NULL) {
// 해당 위치까지 이동 했으니 그 곳에서 노드를 만듦
BstNode* tmp = (BstNode*)malloc(sizeof(BstNode));
tmp->key = value;
tmp->left = tmp->right = NULL;
return tmp;
}
// Search 과정과 비슷함
if (value < node->key)
node->left = insertNode(node->left, value);
else if (value > node->key)
node->right = insertNode(node->right, value);
else // 이미 key가 트리 안에 있으면
; // 아무 것도 하지 않음
return node;
}트리가 비어있는 경우는 처음부터 트리가 비어있었거나, 위치를 찾은 경우에 해당함
그 위치에서 tmp를 이용하여 노드를 만든다.
이후 재귀적 과정을 통해 노드가 연결 된다.
3. delete
// x값을 delete 과정
BstNode* deleteNode(BstNode* root, int x) {
if (root == NULL)
return NULL;
if (x > root->key)
root->right = delete(root->right);
else if (x < root->key)
root->left = delete(root->left);
else {
// x 노드에 자식이 0개일 경우
if (root->left == NULL && root->right == NULL) {
free(root);
return NULL;
}
// x 노드에 자식이 1개일 경우
else if (root->left == NULL && root->right == NULL) {
// tmp 선언하여 x 노드의 자식 노드를 저장함
BstNode* tmp;
// 오른쪽에 자식이 있는 경우
if (root->left == NULL)
tmp = root->right;
// 왼쪽에 자식이 있는 경우
else
tmp = root->left;
// x 노드 삭제
free(root);
return tmp;
}
// x 노드에 자식이 2개일 경우
else {
// x 노드의 오른쪽 서브트리의 최솟값을 찾아서 tmp에 저장함
BstNode* tmp = findMin(root->right);
// root의 값을 tmp 값으로 변경
root->key = tmp->key;
// 그 최솟값 노드를 삭제함
root->right = delete(root->right, tmp->key);
}
}
return root;
}삭제하고자 하는 노드의 자식 수에 따라 해결방법이 달라지므로 주의해야한다.
자식이 0개인 경우: 그냥 그 노드를 삭제하면 됨
자식이 1개인 경우: 그 노드의 자식 노드를 그 노드의 이전 노드와 이어야 함
자식이 2개인 경우: 그 노드의 오른쪽 서브트리의 최솟값을 그 노드의 값에 저장하고, 기존의 최솟값 노드는 제거하는 과정을 거쳐야 한다.
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] AVL Tree C언어로 구현하기 (Insertion, Delete) (0) | 2024.04.18 |
|---|---|
| [자료구조] 배열과 동적 메모리 할당 in C언어 (0) | 2024.04.13 |
| [자료구조] Binary-Tree 이진 트리 C언어로 구현하기 (0) | 2024.04.06 |
| [자료구조] Doubly Linked List (이중 연결 리스트) C언어로 구현하기 (0) | 2024.03.31 |
| [자료구조] Linked List (연결 리스트) C언어로 구현하기 (노드 순회, 검색, 삽입, 삭제) (0) | 2024.03.31 |
